Introducing i-Computer
There are two main screens for the syntax and presentation of the algebraic expression, and two screens for errors.
| "Syntax error" screen | "Definition Error" screen |
|---|---|
| This is where syntax errors are displayed as you type the expression (click to see all of them) | This is where invalid mathematical definitions are displayed when calculating the expression |
| Definition errors will appear during the calculation of the algebraic expression, and the calculation will stop at the point where the error occurs. | |
| Screen 1: | by keyboard | video |
|---|---|---|
 |
An interactive touch screen where you can syntax and correct the algebraic or arithmetic expression with the keyboard format . To modify or cancel the content, you can use the control buttons.
you might scroll vertically to view the entire screen

|
| Screen 2 | by hand | video |
|---|---|---|
 |
Here the expression is presented as one would write it by hand , in the classic mathematical format. The calculated numerical value is also presented
you might zoom
 and drag
and drag
 a double-tap gesture
a double-tap gesture
 resets the algebraic expression to its default scale and position
resets the algebraic expression to its default scale and position
|
Buttons of specific numbers


xxxxxxxxxxThis button is used for the number φ (phi)φ = 0,618033988749894...

The number king of irrationals!!
...for more information: Geometry(Book 2), Chapter 3, pages 230-233


xxxxxxxxxxThis button is used for the number Φ (Phi)Φ = 1,618033988749894...
The numbers
...for more information: Geometry(Book 2), Chapter 2, pages 249 - 260

Tip
if you see a button (animation) for φ - Φ on your device, then : for φ press the button and for Φ long press the button !!


xxxxxxxxxxThis button is used for the number π (pi)π = 3,14159265358979...

The number π (also known as Archimedes' constant) derives its name from the Greek word 'περιφέρεια' (periphery). It emerged from the effort to calculate the circumference of a circle and represents the constant ratio of a circle’s circumference to its diameter. Because of this, it appears frequently in various mathematical practices and calculations.
However, π is not constructible with a ruler and compass—a fact that was not initially known. The ultimately fruitless effort to achieve this became known in history as the problem of 'squaring the circle.' This challenge became an obsession for many mathematicians (and not only) over more than 1500 years—known as the 'hunters of pi'—as they attempted to calculate more and more of its digits.
Even today, computing additional digits of π remains a benchmark for testing the reliability and performance of supercomputers. The number π is also connected to countless equations and formulas, for example:
...for more information: Geometry(Book 3), Chapter 3, pages 248 - 269



xxxxxxxxxxThis button is used for the number ee = 2,71828182845904...

The number e was named in honor of the mathematician Euler. It was discovered by the Swiss mathematician Jacob Bernoulli on the compound interest problem. It is an irrational number, defined by the limit Euler's identity.
Note
the application uses algorithms to calculate more than 16 correct digits of these numbers ( many times they are used 16 digits, for reasons of uniformity - agreement when combining them with operations and using them in mathematical functions)
Control button
| Buttons | video | video |
|---|---|---|
 this button deletes the entire algebraic expression this button deletes the entire algebraic expression | ||
 this button deletes the last single character but not Mathematical functions "log, cos ... If you want to delete a Mathematical function or a larger part of the algebraic expression look at the video. this button deletes the last single character but not Mathematical functions "log, cos ... If you want to delete a Mathematical function or a larger part of the algebraic expression look at the video. | ||
 this button inserts the blank character (also, it is used in conjunction with the undo button to delete a larger part of the algebraic expression) this button inserts the blank character (also, it is used in conjunction with the undo button to delete a larger part of the algebraic expression) | ||
 this button undoes the last input in the algebraic expression (also, it is used in conjunction with the blank character button to delete a larger part of the algebraic expression ) this button undoes the last input in the algebraic expression (also, it is used in conjunction with the blank character button to delete a larger part of the algebraic expression ) |
rules - guide for the correct syntax of algebraic expressions
Warningthe priority of the operations is:
parentheses
functions
powers
multiplication - division
addition subtraction
Important
If there are actions with the same priority (without parentheses or within the same parentheses) the priority is from left to right
Note
It is allowed to write a number in front of parentheses , specific numbers ( e , π , φ , Φ ), functions without the multiplication symbol !
e.g. 3(3+ 5/4) is the same as
e.g. 3e is the same as
e.g. 3log5 is the same as
Caution
But be careful with the syntax : “π3” -> will be considered a syntax error : “π3”
Also the syntax : (log2+4)5 -> will be considered a syntax error : “)5"
Tip
Don't forget that you can look at the Syntax errors Screen! You should also look at Screen 2 which displays the exact expression.
Note
It is allowed to write a number inside a function without parentheses.
e.g. cos 3 is the same as cos(3)
Caution
But be careful with the syntax : e.g. the syntax log 2 ^3 means ( log 2 )^3
Warning
The functions precede the powers. If you want to write: log (2^3) write it exactly so
Tip
Don't forget that you can always use parentheses! You should also consider look at Screen 2 which displays the exact expression.
Note
It is allowed to write a number with a power or a function without parentheses in the denominator of a fraction.
e.g. 3/3^2^2 is the same as 3/(3^2^2)
e.g. 3/(log 3)^3 ≡ 3/((log 3)^3)
Caution
According to the previous rules. e.g. 3/log 3^3 is defined 3/((log 3)^3)
Warning
The functions precede the powers
Tip
Don't forget that you can always use parentheses! You should also consider look at Screen 2 which displays the exact expression.
degrees & rad

xxxxxxxxxxThe degree is a unit of measurement for angles or arcs in a circle.One degree is equal to 1/360 of a full circle.
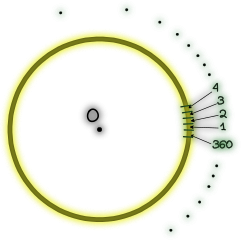
Although circles may differ in size and their degrees "correspond" to different arc , a central angle of a given number of degrees always refers to the same angular size, even though the corresponding arc length varies depending on the radius of the circle. Degrees express a percentage of the circle and are subdivided as follows:
For example, writing
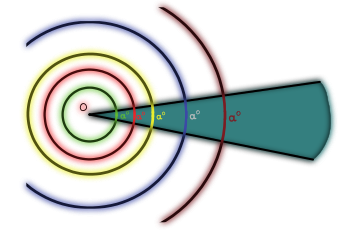
 By default, the input to trigonometric functions is in radians(rad).
By default, the input to trigonometric functions is in radians(rad).
xxxxxxxxxxA radian is equal to an arc that has a length as the radius.
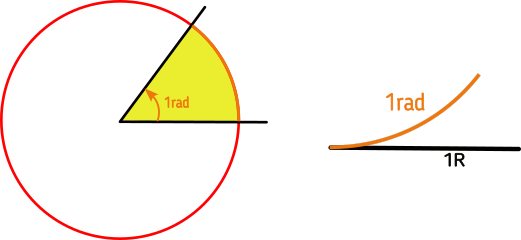
Tip
Don't forget that you can always use rad :
..for more information: Geometry(Book 1), Chapter 1 , pages 60 - 62


